动态规划初探
约 591 字大约 2 分钟
2025-02-17
引入
我们不妨用最朴素的思想来解决这个问题,即暴力枚举
从1出发,我们可以画出这样一副图,可以得到最长为3
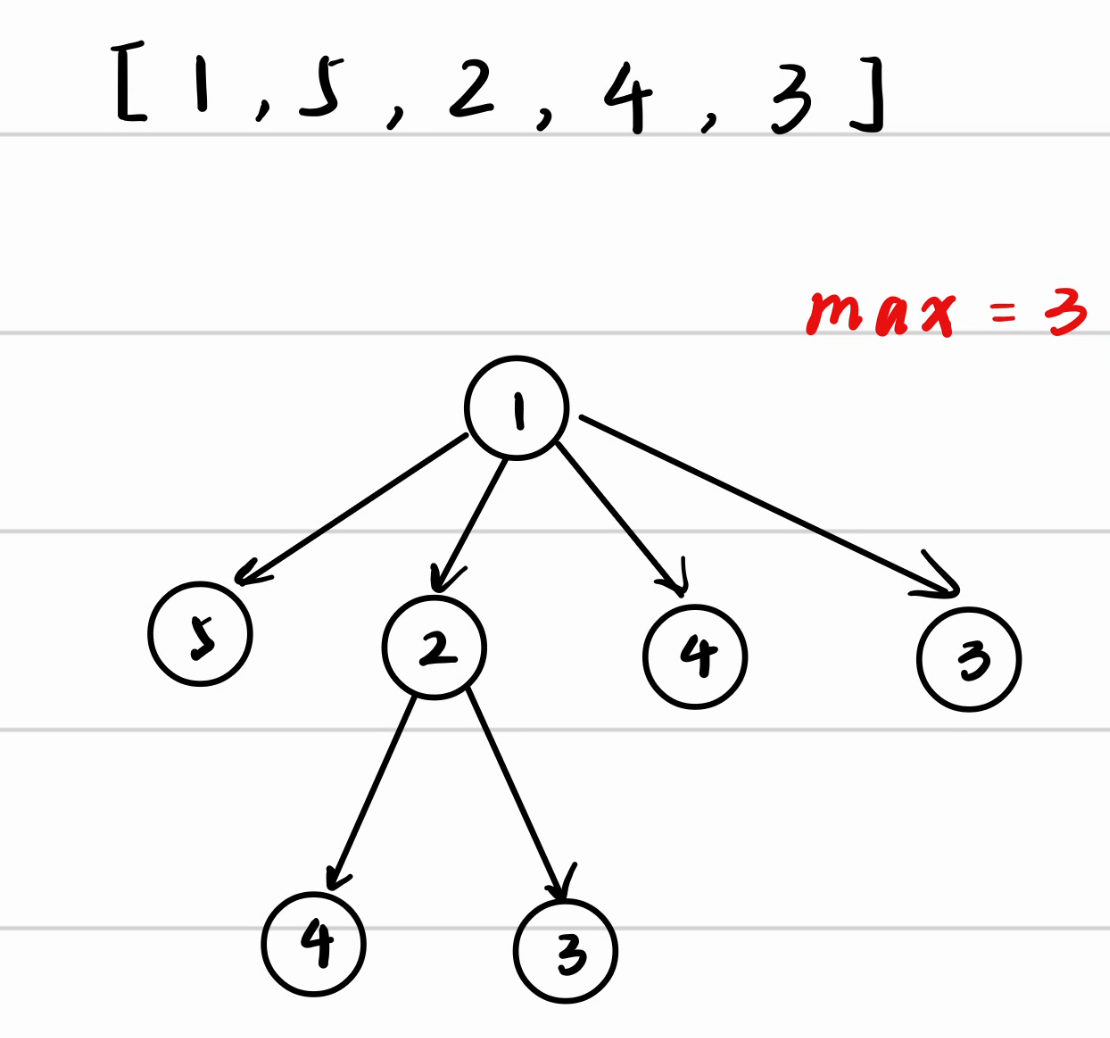
我们对后面几个点进行同样的操作,再更新答案即可。我们可以用递归的思想来编写代码
int dp(vector<int> a, int s) {
int n = a.size();
int ans = 1;
for (int i = s + 1; i < n; i++) {
if (a[i] > a[s]) {
ans = max(ans, dp(a, i) + 1);
}
}
return ans;
}但是,这个算法会遍历每一个子序列(2N),所以它的时间复杂度是指数级的,会超时,我们必须对它进行优化。
我们再次观察这个遍历树,会发现其中存在着大量的重复计算
比如我们在计算1,2,4,就已经计算过从4开始的最大子序列长度,为了避免重复计算,我们可以在第一次计算时,就将结果保留下来。
int dp(vector<int> a, vector<pair<int, bool>>& m, int s) {
int n = a.size();
for (int i = s + 1; i < n; i++) {
if (a[i] > a[s]) {
m[s].first =
max(m[s].first, m[i].second ? m[i].first + 1 : dp(a, m, i) + 1);
}
}
m[s].second = true;
return m[s].first;
}因为使用字典或哈希表保存结果,因此也被称为记忆化搜索,以空间换时间。
非递归
有了的递归的算法,我们还可以将其改写为非递归的形式,这样我们可以更直观地去分析算法的时间复杂度,并且避免了递归时的函数调用开销。
观察之前的计算过程:
dp(0)=max{dp(1),dp(2),dp(3),dp(4)}+1
dp(1)=max{dp(2),dp(3),dp(4)}+1
dp(2)=max{dp(3),dp(4)}+1
dp(3)=max{dp(4)}+1
dp(4)=1
我们可以发现,我们只需要从后往前计算,就可以将所以的答案推算出来。
for (int i = n - 1; i >= 0; i--) {
for (int j = i + 1; j < n; j++) {
if (a[j] > a[i]) m[i] = max(m[i], m[j]);
}
ans = max(ans, ++m[i]);
}我们可以分析出这个算法的复杂度是O(N2)
总结
- 尝试暴力枚举
- 缓存已计算过的值
- 改写递归形式