引入

力扣209题长度最小的子数组

题目概要：给定正整数数组$arr$，目标值$target$，求最小区间，满足$sum \geq target$。

朴素的做法是枚举左右端点$l,r$，然后求区间和，再计算区间最小值，时间复杂度为$O(N^3)$，代码如下

for (int l = 0; l < n; l++) {
    for (int r = l; r < n; r++) {
        int sum = 0;
        for (int i = l; i <= r; i++) sum += arr[i];
        if (sum >= target) ans = min(ans, r - l + 1);
    }
}

而我们学过前缀和，可以知道求区间和只需要$O(1)$，还可以添加一个break进行优化，时间复杂度降为了$O(N^2)$

vector<int> sum(n);
partial_sum(arr.begin(), arr.end(), sum.begin());
auto getSum = [&](int l, int r) {
    if (l == 0) return sum[r];
    return sum[r] - sum[l - 1];
};
for (int l = 0; l < n; l++) {
    for (int r = l; r < n; r++) {
        if (getSum(l, r) >= target) {
            ans = min(ans, r - l + 1);
            break;
        }
    }
}

想要将复杂度降至更低，则需要更厉害的算法，由此引入单调性枚举

解释

观察这张图，我们用二维表来记录不同的$(l,r)$所对应的$case$

其中，绿色注明的点就是break时的点

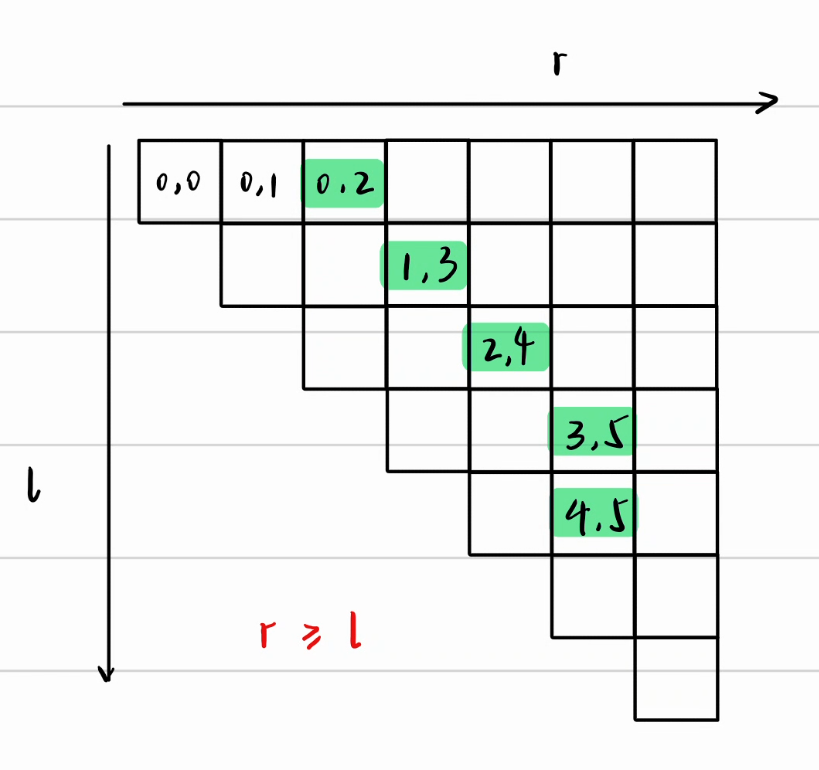
我们不难得到三个规律

1. 高亮格左侧都不满足条件，因为所属区间必然小于满足条件的最小区间
2. 高亮格右侧都满足条件，因为所属区间必然大于满足条件的最小区间（因此我们才可以break）
3. $r$是单调递增的，我们来证明一下：

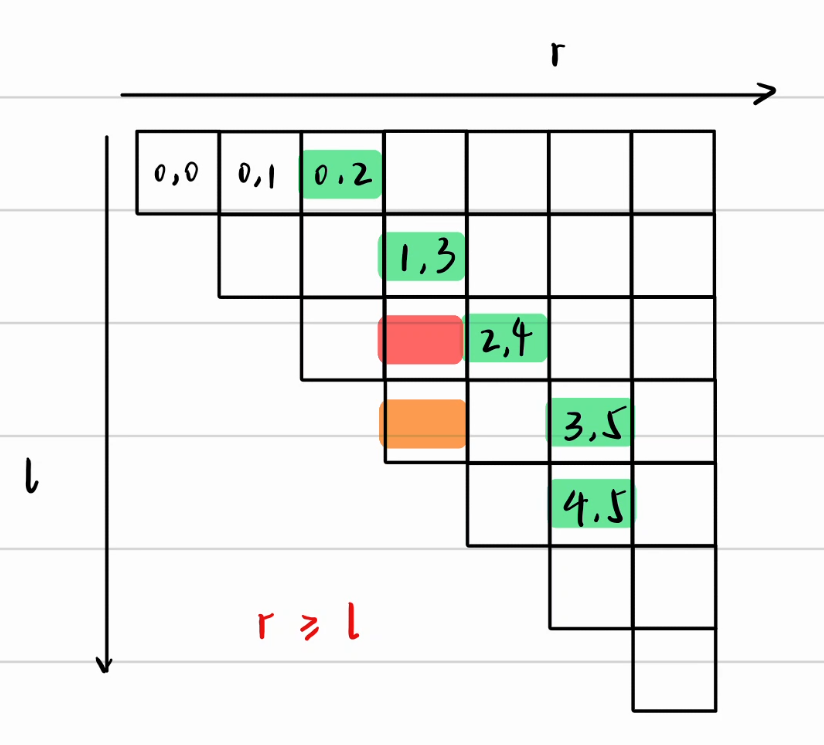
任意选择绿色块左侧的一个红色块，一定不满足条件，而它下面的橙色块区间更小，只有可能比它更不满足条件

所以，对于与红色块同一行的格子来说，只有当$r_{i+1} \geq r_i$，才可能找到满足条件的绿色块

有了这一规律，我们每一次枚举就只需要从上一次的$r$开始枚举即可

vector<int> rightIdx(n);
for (int l = 0; l < n; l++) {
    int r = l == 0 ? 0 : rightIdx[l - 1];
    for (; r < n; r++) {
        if (getSum(l, r) >= target) {
            ans = min(ans, r - l + 1);
            break;
        }
    }
    rightIdx[l] = r;
}

这样，我们就得到了复杂度为$O(N)$的算法

提示

在这个图中，行进路线一定是往右或往下的，最多遍历$2N$个位置

推广

我们还可以更进一步地优化这个代码

将$r$定义在外层，使其在整个枚举期间不会被重置

for (int l = 0, r = 0; l < n; l++) {
    for (; r < n; r++) {
        if (getSum(l, r) >= target) {
            ans = min(ans, r - l + 1);
            break;
        }
    }
}

更进一步，我们不需要计算前缀和，可以在枚举时维护区间的关键值

int sum = 0;
for (int l = 0, r = 0; l < n;) {
    if (r < n && sum < target)
        sum += arr[r++];
    else {
        if (sum >= target) ans = min(ans, r - l);
        sum -= arr[l++];
    }
}

如果$r$可以继续前进，并且关键值不满足条件，那么$r$就往前，否则$l$往前

如果关键值满足条件，则更新答案

重点可以归为四步：

1. 判断是否满足条件

2. 增加一个元素时，如何维护区间关键值

3. 删除一个元素时，如何维护区间关键值

4. 找到满足的条件时，如何更新答案

我们可以把这四步抽象为一个模板函数

template<typename M, typename I, typename R, typename U>
void increaseEnumerate(int s, int e,
                       const M& match,
                       const I& insert,
                       const R& remove,
                       const U& update) {
    for (int l = s, r = s; l <= e; ) {
        if (l < r && match(l, r - 1)) {
            update(l, r - 2);
            remove(l++, r);
        } else if (r <= e) {
            insert(l, r++);
        } else {
            update(l, r - 1);
            remove(l++, r);
        }
    }
}

返回的区间为不满足条件的最大区间，因为这样可以应对很多种不一样的情况。

这个最大区间，是当$l$确定，使得不能满足条件时，$r$取得最大，我们需要这个$r$单调递增。

即增加一个元素，只可能使条件由不满足变为满足，而不可能使条件由满足变为不满足。 减少一个元素，只可能使得条件由不满足变为满足，而不可能使条件由不满足变为满足。

拓展

由单调递增模型，我们也可以得出单调递减模型。

力扣167题两数之和II-输入有序数组

for (int l = 0, r = n - 1; l < r;) {
    if (numbers[l] + numbers[r] >= target) {
        if (numbers[r] + numbers[l] == target) ans = {l + 1, r + 1};
        r--;
    } else {
        l++;
    }
}

这道题还能从另一种角度思考，通过单调性来减少枚举次数，称为单调性剪枝

for (int l = 0, r = n - 1; l < r;) {
    if (numbers[l] + numbers[r] > target) {
        r--;
    } else if (numbers[l] + numbers[r] < target) {
        l++;
    } else {
        ans = {l + 1, r + 1};
        break;
    }
}

难点

单调性的条件和题目要求条件可能不一致，在做题时需要灵活转化！！